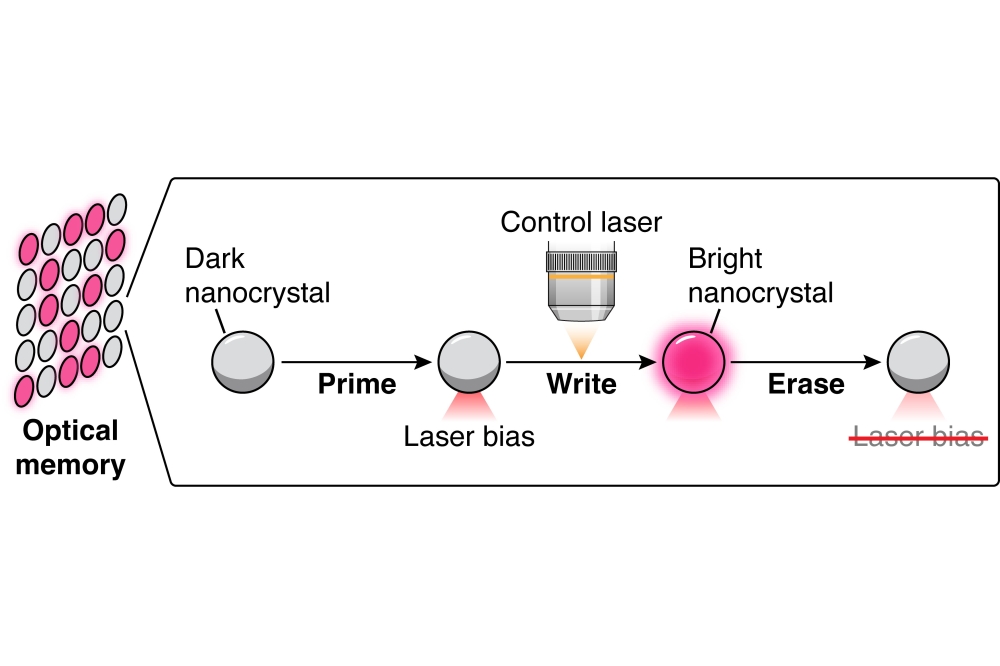
Broadband PICs with 3 µm SOI technology
Micrometer-scale silicon waveguides enable ultra-broadband PICs with low coupling losses.
By Timo Aalto, VTT Technical Research Centre of Finland
Based on photonics textbooks, many would say that an optical waveguide with 3 µm thick silicon core is highly multi-moded, requires >>1 mm bending radius and suffers from strong back-reflections at input/output facets. In other words, such micrometer-scale silicon waveguides would not be suitable for making dense photonic integrated circuits (PICs). By thinking beyond the obvious, all these assumptions have been proven wrong, and the 3 µm thick silicon-on-insulator (SOI) waveguide technology has been used to demonstrate compact PICs with ultra-broadband, polarization independent low-loss operation (Fig. 1).
The development and commercialization of silicon photonics has taken huge steps in the past 10 years. Most of the work has been done with sub-micrometer waveguides, typically 220-300 nm thick, which can be processed in CMOS foundries that have been built for the production of electronic integrated circuits (EICs). This enables easy scaling to large-volume production without the need to invest into new foundries. Another advantage of the “thin-SOI” waveguides is that they comply with the photonics textbooks in terms of single-mode (SM) operation and small bending radii. Grating couplers and inverse tapers also allow to couple light in/out without significant back-reflections. The term “high-confinement” is often used to describe the ability to confine light into small mode-field (cross-section) areas with the help of the large refractive index contrast between silicon and silicon dioxide.
However, for a single-mode 220 nm SOI waveguide, the relative confinement of the fundamental mode’s optical power into the Si core is approximately the same as in a standard single mode fiber (SMF) This is because the waveguide design matches the size of the rectangular core to the refractive index contrast to stay close to the SM-limit. For a 220 x 500 nm SOI waveguide the confinement at 1550 nm wavelength is ~76 % for the horizontal (TE) polarization and ~43 % for the vertical (TM) polarization, while it is ~73% for a SMF. Because of the large geometrical birefringence, the thin SOI waveguides are typically used with one polarization only.
Fig. 1: Schematic illustration of the 3 µm SOI waveguide platform.
In a 3 µm thick SOI waveguide the cross-section area of the fundamental mode is naturally larger, but the relative confinement of the mode inside the waveguide core is much higher (99.96% for both TE and TM). This ultra-high mode confinement leads to many exceptional waveguide properties.
Firstly, the 3 µm SOI waveguides become quite insensitive to variations in the waveguide dimensions and wavelength. The effective index of the fundamental mode remains very close to the refractive index of bulk silicon even if the waveguide width or height is changed by a few %. This leads to small phase errors in the PICs and allows to realize e.g. optical phased arrays (OPAs) and cascaded interferometers without phase modulators and complex electrical control circuits.
The mode confinement remains high even if the wavelength is doubled (Fig. 2). This means that the same 3 µm SOI waveguide works well from 1.2 µm (lower limit from the energy gap of Si) to >3 µm wavelength where the absorption of the silicon dioxide cladding starts to become a limitation. High confinement actually helps to push further the upper wavelength limit since only a small fraction of the light propagates in the absorbing SiO2 cladding even at 3 µm wavelength. By replacing SiO2 with some other cladding material it is possible to further extend the wavelength range to ~6 µm where multi-phonon absorption starts to become a limiting factor.
Fig. 2: Simulated mode fields of square-shaped 3 µm SOI waveguides at 1.2 and 3 µm wavelength, and at both polarizations.
Secondly, ultra-high mode confinement enables polarization-independent operation (Fig. 2). With an approximately square waveguide cross-section it is possible to have exactly zero-birefringence operation, and the birefringence remains small for other waveguide shapes as well. This opens up the possibility to make polarization independent and dual-polarization PICs with 3 µm SOI waveguides.
Thirdly, the ultra-high mode confinement leads to very low propagation losses. Between 1.2 and 3 µm wavelengths, the waveguide absorption is negligible and the propagation loss comes from mode field scattering at the dry-etched waveguide side-walls. This scattering loss depends on the overlap of the mode field with the roughness on the waveguide side-wall, which is extremely small in the 3 µm SOI waveguides. By replacing thermal oxidation with hydrogen annealing (Fig. 3), the side-wall roughness has been reduced to a few nm, which leads to a few dB propagation loss per meter. In meter-long waveguide spirals the propagation loss has been demonstrated to be ~4 dB/m, which includes the bending losses. In race-track ring resonators the intrinsic quality (Q) factors have reached >10 million, which corresponds to propagation losses <3 dB/m inside the ring [1]
Fig. 3: The propagation losses of the 3 µm SOI waveguides are reduced to a few dB per meter by using hydrogen annealing to smoothen the waveguide side-walls.
The fourth advantage of the ultra-high mode confinement is the ability for ultra-dense integration (Fig. 4). Historically, the micron-scale waveguides required bending radii of millimeters or even centimeters. This limitation was first eliminated with total-internal reflection mirrors, which had an effective bending radius smaller than the width of the waveguide. They are still the preferred approach for extremely dense integration, although they have an insertion loss of ~0.1 dB/90° for turning the light. Waveguides with lower confinement can't reach as low loss because the light propagating in the cladding doesn't get reflected by the mirror.
A practically lossless approach then appeared in the form of an Euler bend that has negligible (<0.001 dB/90°) loss, as long as the bending radius is at least a few µm [2]. In addition to small bends and mirrors, the high confinement allows the realization of trivial waveguide crossings where light barely sees an intersecting waveguide.